The complete characterization of a deformable body requires both its translational and rotational measurements, which are usually termed as six-degree-of-freedom (6-DOF) motions. Translational signals have been studied routinely for seismic events. But unfortunately, coseismic rotational motions cannot be easily directly recorded at present due to limitations of technique. Alternatively, they can be indirectly measured using a dense seismic array according to linear elasticity theory by presuming a spatially uniform rotational pattern over the extent of the array at the cost of permanent information. In 2013, we proposed a new seismogeodetic approach to measure coseismic ground tilts at a single point by combining collocated high-rate GPS and accelerometer measurements in a Kalman filter which could identified the tilts with a precision of 0.01°including permanent information . With the availability of the first generation of commercial rotational sensors R1 and its updated version R2, in 2019, we further developed our approach by incorporating gyroscope data into the Kalman filter and then estimating Euler angles to quantify instrument rotations. With this super collocation of high-rate GNSS, accelerometers, and gyroscopes, we find that the displacement and rotation waveforms can be more accurately recovered over a very broad frequency band inclusive of 0 Hz in theory.
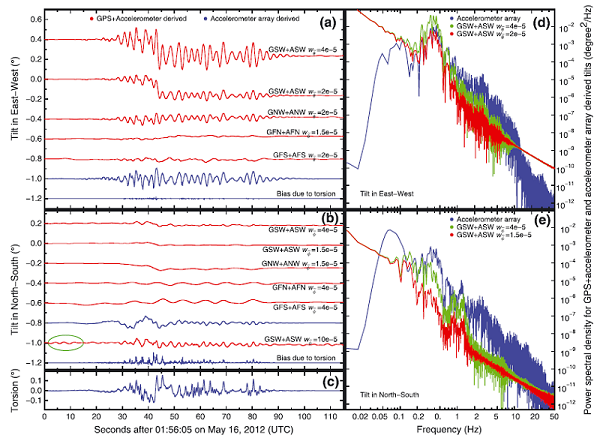
Fig.1 (a–c) Coseismic point pseudotilts and (d and e) their power spectral densities derived from collocated GPS+accelerometers for a simulated seismic event using shake table. Also shown are the rotation estimates from the four-accelerometer array on the roof. The red traces in Fig 1a and 1b are labeled with the collocation pairs and the applied standard deviations of process noise of pseudotilts. The green open ellipse highlights spurious pre-event pseudotilts. All traces in Fig 1a and 1b are offset by 0–12 multiples of 0.1° for clarity. The “Bias due to torsion” in the E-W and N-S pseudotilts are computed with An/(Au–g) and Ae/(Au–g) , respectively, based on the accelerometer array derived torsions (Fig 1c). In Fig 1d and 1e, the blue, green, and red traces correspond to the accelerometer array derived tilts, the GSW+ASW derived pseudotilts, respectively. This figure shows that with collocated GPS+accelerometers, we can recover point tilts including permanent information with high precision.
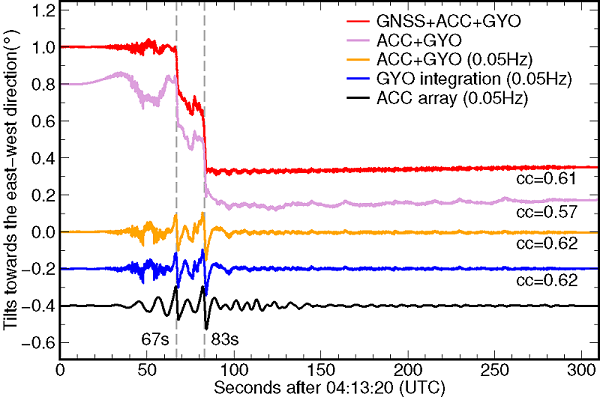
Fig.2 Tilts toward the east-west direction derived from the six-degree-of-freedom seismogeodetic combination, the six-degree-of-freedom inertial combination, the integration of gyroscope data, and the array of accelerometer data for a simulated sesimic event using shake table. All solutions are offset arbitrarily to avoid overlap. “0.05 Hz” in parentheses means a high-pass filter with a corner frequency of 0.05 Hz. “cc” abbreviates the “correlation coefficient” between the accelerometer-array derived tilts and all others; note that such coefficients are calculated for “GNSS + ACC + GYO” and “ACC + GYO” by preapplying a 0.05-Hz high-pass filter on their tilts. This figure shows precise rotational motions can be obtained by our proposed six-degree-of-freedom.
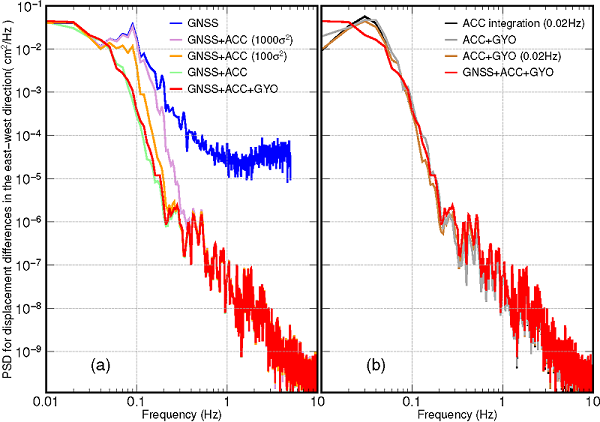
Fig.3 Power spectral densities (PSDs over 0.01–10 Hz, cm2/Hz) of the differences between the shake table recordings and other solutions. We made two panels for clarity of PSDs and thus the“GNSS + ACC + GYO” solution is plotted twice; (a) shows the seismogeodetic solutions, while (b) shows the inertial solutions. GNSS = Global Navigation Satellite Systems. This figure shows with our six-degree-freedom seismogeodesy approach precise broadbrand displacements can be derived.
Related Works
1. Geng J*, Melgar D, Bock Y, Pantoli E, Restrepo, J (2013) Recovering coseismic point ground tilts from collocated high-rate GPS and accelerometers. Geophys. Res. Lett., 40, 5095-5100, doi:10.1002/grl.51001
2. Geng J*, Wen Q, Chen Q, Chang H (2019) Six-degree-of-freedom broadband seismogeodesy by combining collocated high-rate GNSS, accelerometers and gyroscopes. Geophys. Res. Lett. 46(2):708-716, doi:10.1029/2018GL081398
Copyright PRIDELAB IN GNSS CENTER , Wuhan University Visits:172820 Powered by Truesing